引言
监督学习
- 根据数据集中的样本的“正确答案”,设法预测出未知数据的正确答案。
- 回归问题,即通过回归来推出一个连续的输出。
- 分类问题,对目标分类,输出离散结果。
无监督学习
对于没有分类或标签的数据集,找到其中的某种数据结构,或者将其分类。
单变量线性回归(Linear Regression with One Variable)
模型
- 回归问题中,输入变量只有一个,通过给定数据,建立回归模型,类似一元函数,进行预测,使代价函数最小。
- 假设函数,对给地值进行预测,通常表示为小写 $h$ 表示。 $h_\theta \left( x \right)=\theta_{0} + \theta_{1}x$,
代价函数
- 代价函数也被称作平方误差函数,是预测值和实际值之间误差的平方和。
参数(parameters)$\theta_{0}$ 和 $\theta_{1}$,假设函数 $h_\theta \left( x \right)=\theta_{0} + \theta_{1}x$,真实结果$y{(i)}$,有如下代价函数:
$J \left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_m \left( h_{\theta}(x{(i)})-y{(i)} \right)^{2}$
优化的目标就是降低代价函数的值
梯度下降算法
梯度下降是一个用来求函数最小值的算法,梯度下降算法可用来求出代价函数$J(\theta_{0}, \theta_{1})$ 的最小值。
梯度下降背后的思想是:开始时我们随机选择一个参数的组合$\left( {\theta_{0}},{\theta_{1}},......,{\theta_} \right)$,计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。
相当于,你站在山上想要快速下山,你要观察自己一周,找到下降最快的那个方向,走出一步,然后再观察自己一周,再找到下降最快的那个方向,再走出一步。重复上面步骤,直到接近局部最低点。
- ${\theta_}={\theta_}-\alpha \frac{\partial }{\partial {\theta_}}J\left( \theta \right)$
{% note warning %}
${\theta}$在一次迭代中需要同步更新,例如
$={\theta_{0}}-\alpha \frac{\partial }{\partial {\theta_{0}}}J\left( \theta \right)$
$={\theta_{1}}-\alpha \frac{\partial }{\partial {\theta_{1}}}J\left( \theta \right)$
${\theta_{0}}=$
${\theta_{1}}=$
{% endnote %}
$\alpha$ 是学习率(learning rate),它决定了梯度下降的快慢。
如果$a$太小了,即学习速率太小,这样就需要很多步才能到达最低点,如果$a$太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛,下一次迭代又移动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来越远,所以,如果$a$太大,它会导致无法收敛,甚至发散。
多变量线性回归(Linear Regression with Multiple Variables)
多变量线性回归与单变量类似,也是要找出使得代价函数最小的一系列参数。
特征缩放
面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。
最简单的方法是令:${x_}= \frac {x_-{\mu_}}{s_}$,其中 ${\mu_}$是平均值,${s_}$是标准差。
通常可以考虑尝试些学习率:$\alpha=0.01,0.03,0.1,0.3,1,3,10$
正规方程
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的:$\frac{\partial}{\partial{\theta_}}J\left( {\theta_} \right)=0$ 。
假设我们的训练集特征矩阵为 $X$(包含了 ${x_{0}}=1$)并且我们的训练集结果为向量 $y$,则利用正规方程解出向量
$\theta =\left( XTX \right){-1}{X^}y$ 。
上标T代表矩阵转置,上标-1 代表矩阵的逆。
只要特征变量的数目并不大,标准方程是一个很好的计算参数 $\theta$ 的替代方法。具体地说,只要特征变量数量小于一万,推荐使用标准方程法。
逻辑回归(Logistic Regression)
分类问题
逻辑回归 (Logistic Regression) 算法,尝试预测的是结果是否属于某一个类(例如正确或错误)。
对于二元的分类问题,我们将因变量(dependent variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class),则因变量$y\in { 0,1 \}$ ,其中 0 表示负向类,1 表示正向类。
假说表示
当${h_\theta}\left( x \right)>=0.5$时,预测 $y=1$。
当${h_\theta}\left( x \right)<0.5$时,预测 $y=0$ 。
我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在0和1之间。
逻辑回归模型的假设是: $h_\theta \left( x \right)=g\left(\thetaX \right)$
其中:
$X$ 代表特征向量
$g$ 代表逻辑函数(logistic function)
一个常用的逻辑函数为S形函数(Sigmoid function),公式为: $g\left( z \right)=\frac{1}{1+e{-z}}$。
$h_\theta \left( x \right)$的作用是,对于给定的输入变量,根据选择的参数计算输出变量=1的可能性(estimated probablity)即$h_\theta \left( x \right)=P\left( y=1|x;\theta \right)$
例如,如果对于给定的$x$,通过已经确定的参数计算得出$h_\theta \left( x \right)=0.7$,则表示有70%的几率$y$为正向类,相应地$y$为负向类的几率为1-0.7=0.3。
代价函数
我们重新定义逻辑回归的代价函数为:$J\left( \theta \right)=\frac{1}\sum\limits_{Cost\left( {h_\theta}\left({\left( i \right)} \right),^{\left( i \right)} \right)}$,其中
$Cost\left( {h_\theta}\left( x \right),y \right)=\begin
-log\left( {h_\theta}\left( x \right)\right) &&
-log\left( 1-{h_\theta}\left( x \right) \right) &={1},\&={0}
\end$ 简化如下:
$Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right)$
在得到这样一个代价函数以后,我们便可以用上文中的梯度下降算法来求得能使代价函数最小的参数了。
代入代价函数得到:
$J\left( \theta \right)=-\frac{1}\sum\limits_^{[{y{(i)}}\log \left( {h_\theta}\left( {x{(i)}} \right) \right)+\left( 1-{y{(i)}} \right)\log \left( 1-{h_\theta}\left( {x{(i)}} \right) \right)]}$
推导得
$J\left( \theta \right)=-\frac{1}\sum\limits_[-{y{(i)}}\log \left( 1+{e{-{\thetaT}{x{(i)}}}} \right)-\left( 1-{y{(i)}} \right) \log \left( 1+{e{\thetaT}{x^{(i)}}} \right)]$
$\frac{\partial }{\partial {\theta_}}J\left( \theta \right)=\frac{1}\sum\limits_{[{h_\theta}\left( {x{(i)}} \right)-{y{(i)}}]x_j{(i)}}$
多类别分类:一对多
多分类就是将多个二元分类结合起来。
正则化(Regularization)
过拟合的问题
过拟合(over-fitting)问题,如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为0),但是可能会不能推广到新的数据。由于过于强调拟合原始数据,而丢失了算法的本质:预测新数据。
正则化(regularization)技术,它可以改善或者减少过度拟合问题。
代价函数
正则化的基本方法就是减小参数θ 的值。
假如我们有非常多的特征,我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设:
$J\left( \theta \right)=\frac{1}{2m}[\sum\limits_{({h_\theta}({x{(i)}})-{y{(i)}})2}+\lambda \sum\limits_{\theta_{2}}]$
神经网络:表述(Neural Networks: Representation)
模型表示
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元(也叫激活单元,activation unit)采纳一些特征作为输出,并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例,在神经网络中,参数又可被成为权重(weight)。
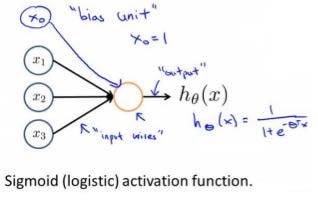
类似于神经元的神经网络,效果如下:
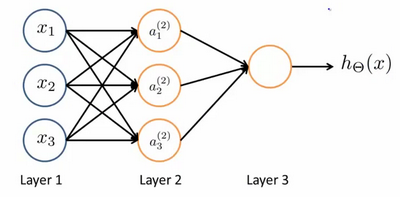
- 其中$x_1$, $x_2$, $x_3$是输入单元(input units),我们将原始数据输入给它们。
- $a_1$, $a_2$, $a_3$是中间单元,它们负责将数据进行处理,然后呈递到下一层。
- 最后是输出单元,它负责计算${h_\theta}\left( x \right)$。
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络,第一层成为输入层(Input Layer),最后一层称为输出层(Output Layer),中间一层成为隐藏层(Hidden Layers)。我们为每一层都增加一个偏差单位(bias unit):
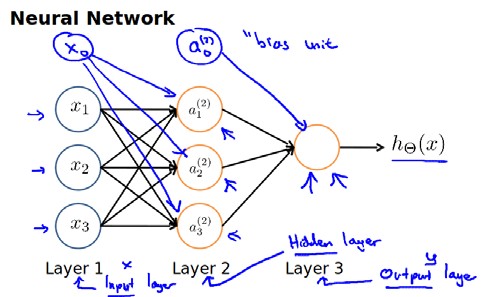
下面引入一些标记法来帮助描述模型:
$a_{\left( j \right)}$ 代表第$j$ 层的第 $i$ 个激活单元。${\theta {\left( j \right)}}$代表从第 $j$ 层映射到第 $j+1$ 层时的权重的矩阵,例如${\theta {\left( 1 \right)}}$代表从第一层映射到第二层的权重的矩阵。其尺寸为:以第 $j+1$层的激活单元数量为行数,以第 $j$ 层的激活单元数加一为列数的矩阵。例如:上图所示的神经网络中${\theta {\left( 1 \right)}}$的尺寸为 3*4。
对于上图所示的模型,激活单元和输出分别表达为:
$a_{1}{(2)}=g(\Theta _{10}{(1)}{x_{0}}+\Theta {11}^{(1)}{x{1}}+\Theta {12}^{(1)}{x{2}}+\Theta {13}^{(1)}{x{3}})$
$a_{2}{(2)}=g(\Theta _{20}{(1)}{x_{0}}+\Theta {21}^{(1)}{x{1}}+\Theta {22}^{(1)}{x{2}}+\Theta {23}^{(1)}{x{3}})$
$a_{3}{(2)}=g(\Theta _{30}{(1)}{x_{0}}+\Theta {31}^{(1)}{x{1}}+\Theta {32}^{(1)}{x{2}}+\Theta {33}^{(1)}{x{3}})$
${h_{\Theta }}(x)=g(\Theta {10}^{(2)}a{0}{(2)}+\Theta _{11}{(2)}a_{1}{(2)}+\Theta _{12}{(2)}a_{2}{(2)}+\Theta _{13}{(2)}a_{3}^{(2)})$
我们可以知道:每一个$a$都是由上一层所有的$x$和每一个$theta$所对应的决定的。
(我们把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION ))
把$x$, $\theta$, $a$ 分别用矩阵表示:
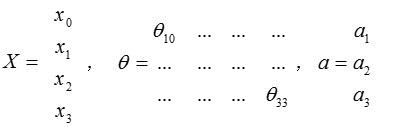
我们可以得到$\theta \cdot X=a$ 。
利用向量化的方法会使得计算更为简便。以上面的神经网络为例,试着计算第二层的值:
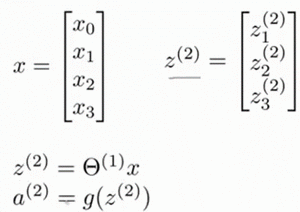

我们令 ${z{\left( 2 \right)}}={\theta {\left( 1 \right)}}x$,则 ${a{\left( 2 \right)}}=g({z{\left( 2 \right)}})$ ,计算后添加 $a_{0}^{\left( 2 \right)}=1$。 计算输出的值为:
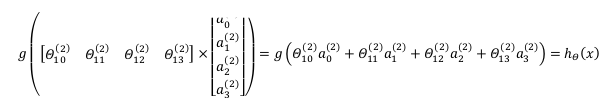
我们令 ${z{\left( 3 \right)}}={\theta{\left( 2 \right)}}{a{\left( 2 \right)}}$,则 $h_\theta(x)={a{\left( 3 \right)}}=g({z{\left( 3 \right)}})$。
这只是针对训练集中一个训练实例所进行的计算。如果我们要对整个训练集进行计算,我们需要将训练集特征矩阵进行转置,使得同一个实例的特征都在同一列里。即:
${z{\left( 2 \right)}}=\Theta{\left( 1 \right)}\times X$
${a{\left( 2 \right)}}=g({z{\left( 2 \right)}})$
例子:AND
我们可以用这样的一个神经网络表示AND 函数:
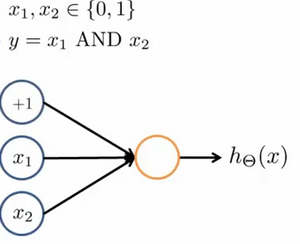
其中$\theta_0 = -30, \theta_1 = 20, \theta_2 = 20$
我们的输出函数$h_\theta(x)$即为:$h_\Theta(x)=g\left( -30+20x_1+20x_2 \right)$
我们知道$g(x)$的图像是:
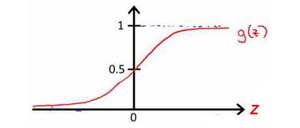

所以我们有:$h_\Theta(x) \approx \text_1 \text , \text_2$ ,这就是AND函数。
神经网络的学习(Neural Networks: Learning)
反向传播算法(bp)
为了计算代价函数的偏导数$\frac{\partial}{\partial\Theta^{(l)}_}J\left(\Theta\right)$,我们需要采用一种反向传播算法。
-
使用正向传播方法,我们从第一层开始正向一层一层进行计算,得到各个 $a_^{\left( j \right)}$ 的值,直到最后一层的$h_{\theta}\left(x\right)$,例如
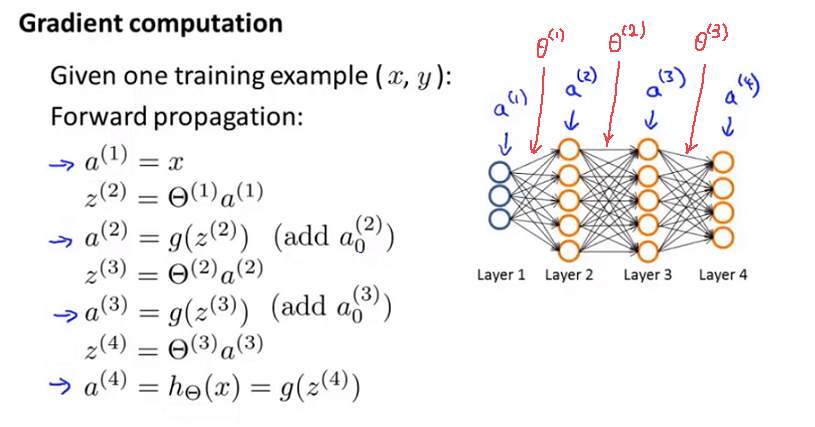
-
对于输出层的每个输出单元,计算误差。用$\delta_{(n_l)}$来表示误差,则:$\delta_{(n_l)}=a_^{(n_l)}-y_$
-
计算各层误差,对于$l = n_l-1 ,n_l -2 ,..., 2$ :$\delta{(l)}=\left({\Theta{(l)}}\right)\delta{(l+1)}\ast g'\left(z{(l)}\right)$其中 $g'(z{(l)})$是 $S$ 形函数的导数,$g'(z{(l)})=a{(l)}\ast(1-a{(l)})$。而$(θ{(l)})\delta{(l+1)}$则是权重导致的误差的和。
($\delta=\frac{\partial}{\partial z{(l)}}J(\Theta)$) -
计算代价函数的偏导数,假设$λ=0$,即我们不做任何正则化处理时有:
$\frac{\partial}{\partial\Theta_{(l)}}J(\Theta)=a_{(l)} \delta_^{l+1}$
梯度检验
梯度的数值检验(Numerical Gradient Checking)方法。这种方法的思想是通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。
对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的 $\theta$,我们计算出在 $\theta$ - $\varepsilon$ 处和 $\theta$ + $\varepsilon$ 的代价值($\varepsilon$是一个非常小的值,通常选取 0.001),然后求两个代价的平均,用以估计在 $\theta$ 处的代价值。
随机初始化
如果我们令所有的初始参数都为0,这将意味着我们第二层的所有激活单元都会有相同的值。同理,如果我们初始所有的参数都为一个非0的数,结果也是一样的。
我们通常初始参数为正负ε之间的随机值。
关于理论知识的学习暂告一段落
